GetFEMによるElliptic Membraneベンチマークテスト#
GetFEMによるElliptic Membraneベンチマークテストというタイトルでお話をさせていただきます。
背景と動機#
まずは、背景について説明させていだきます。 現在、FEABerというプロジェクトに参加しています。 このプロジェクトは複数のオープンソースプロジェクトの FEAコードをベンチマークするプロジェクトです。 ベンチマークテストは The Standard NAFEMS Benchmarks から引用しています。 参加プログラムにはCalculiX, Code-Aster, FrontISTR があります。 この発表ではそれらの結果とGetFEMの結果を比べた途中経過を報告したいと思います。 ベンチマークテストの解析にPythonスクリプトを使用していますが、今回はそれらについても詳細に解説いたします。
問題の説明#
今回対象とした問題は The Standard NAFEMS Benchmarks に LE1 として掲載されている問題です。 圧力を負荷された楕円形状に発生する応力を確認するベンチマークになっています。
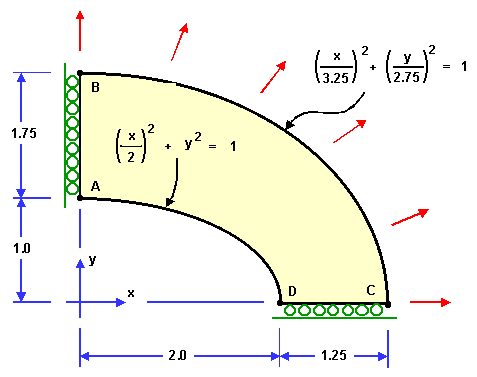
入力する物性値は次の通りです。
材料物性 |
入力値 |
|---|---|
ヤング率 |
210000 MPa |
ポアソン比 |
0.3 |
要素種別 |
平面応力要素 |
厚さ |
0.1 mm |
メッシュ作成#
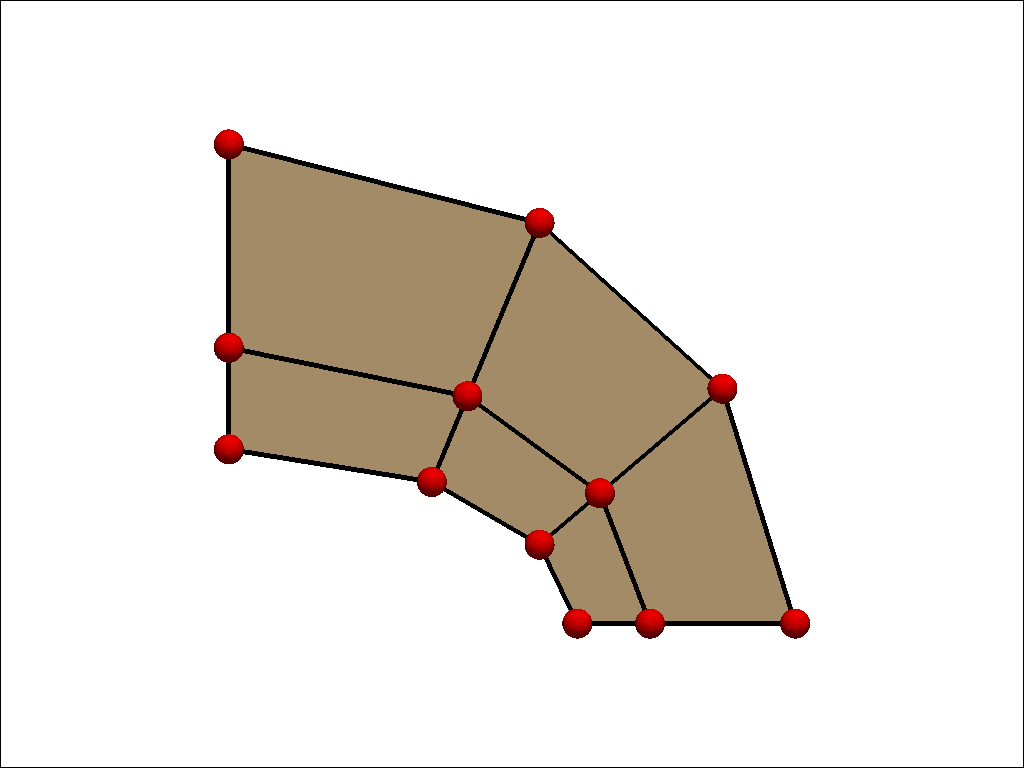
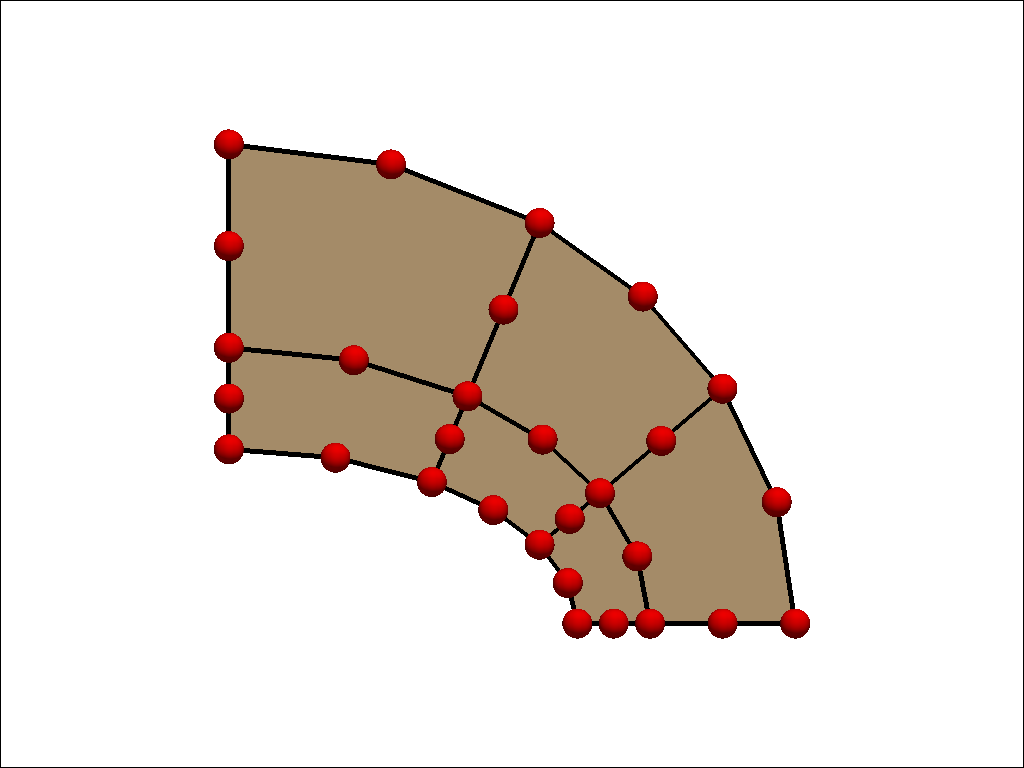
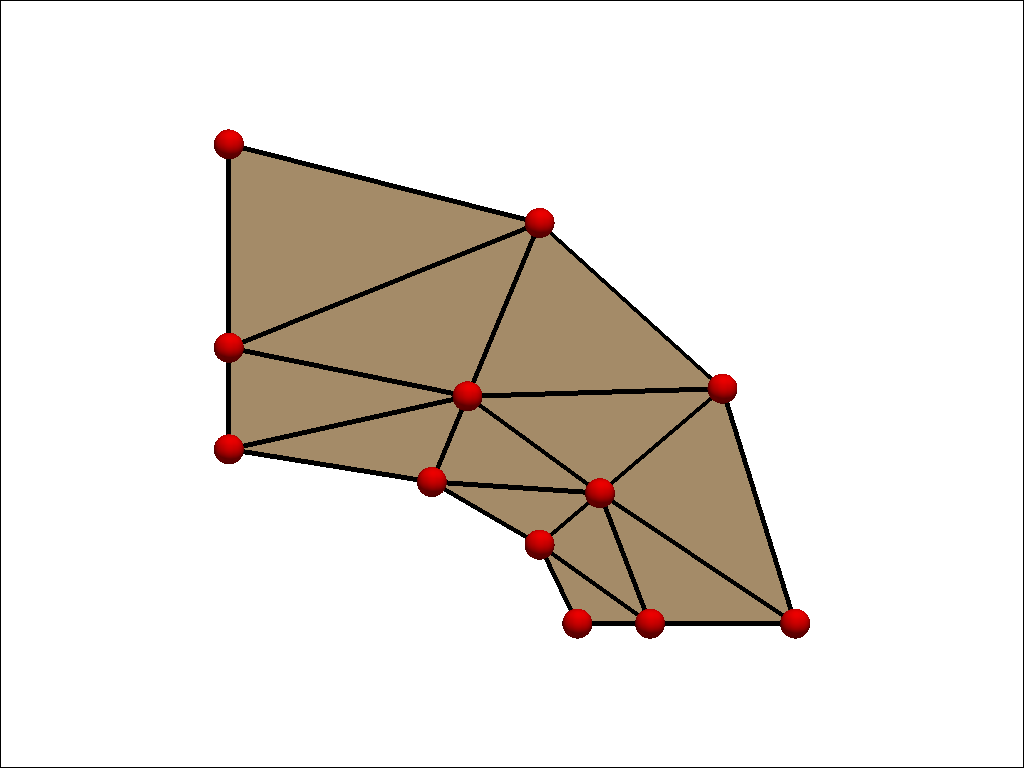
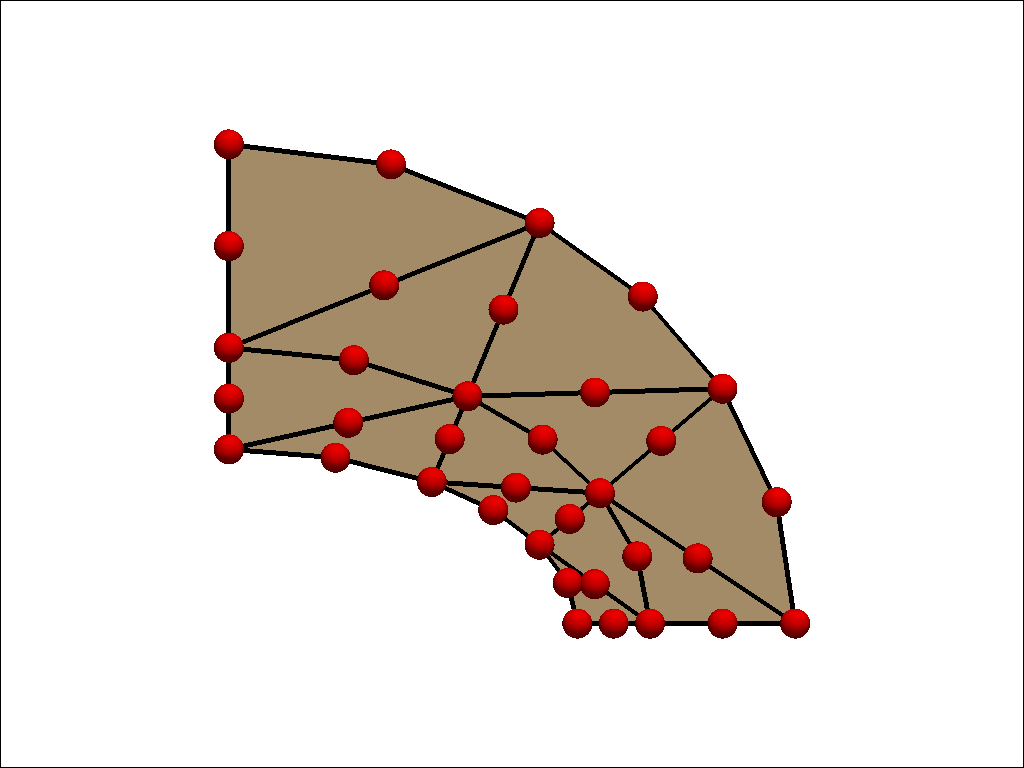
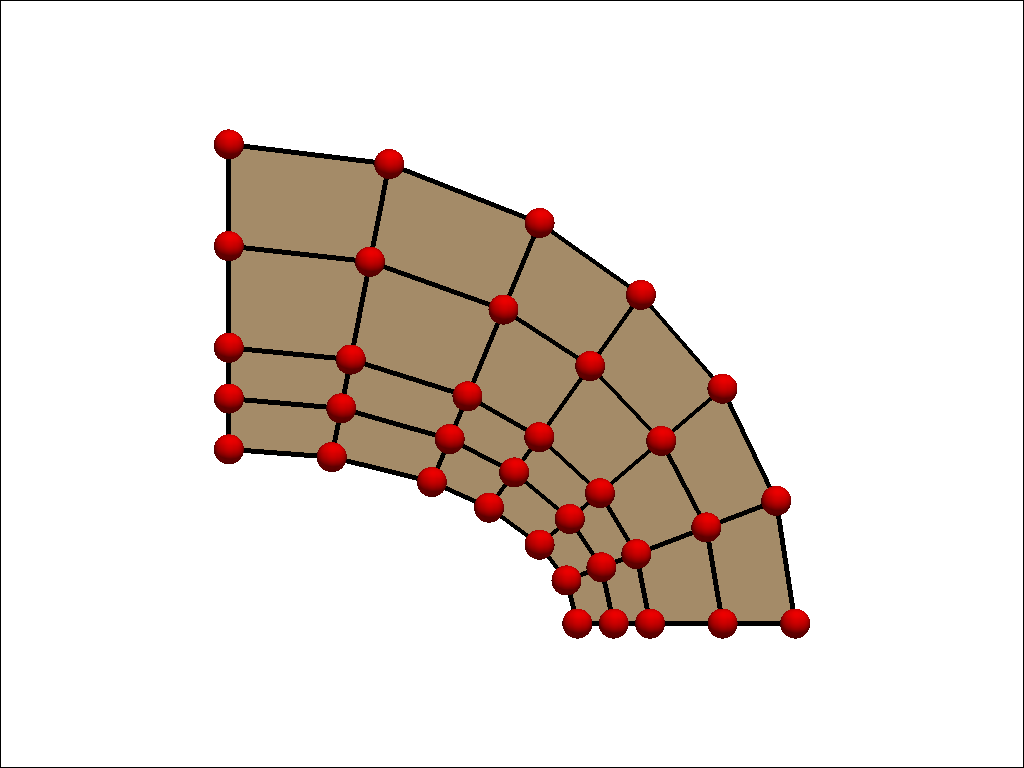
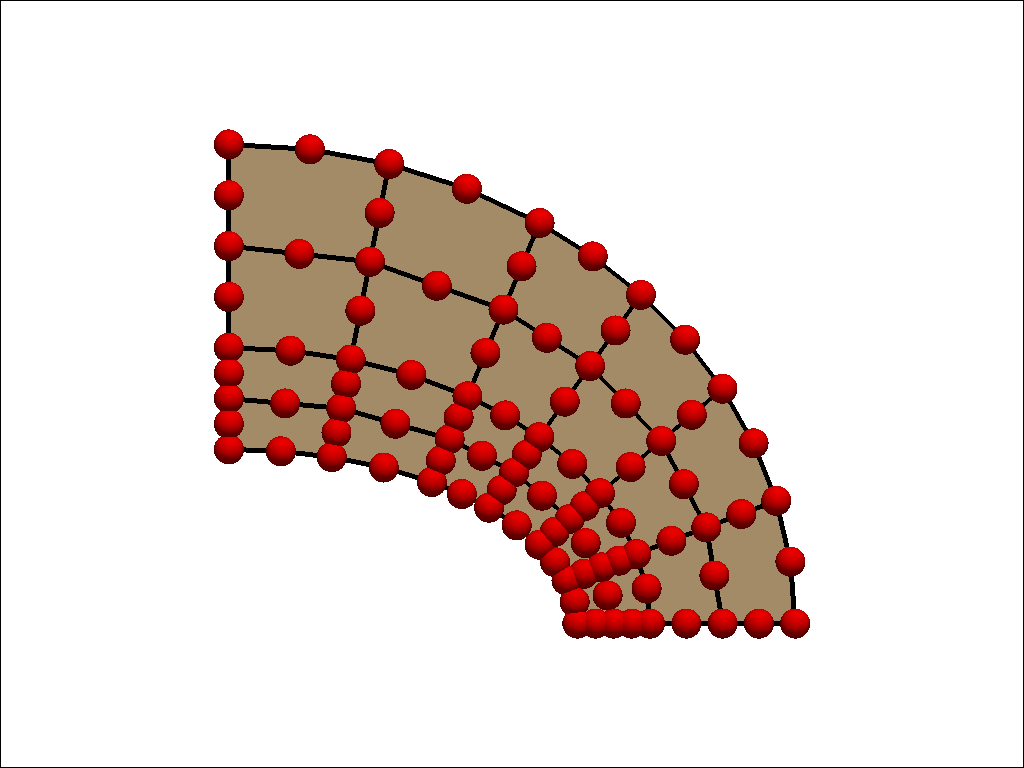
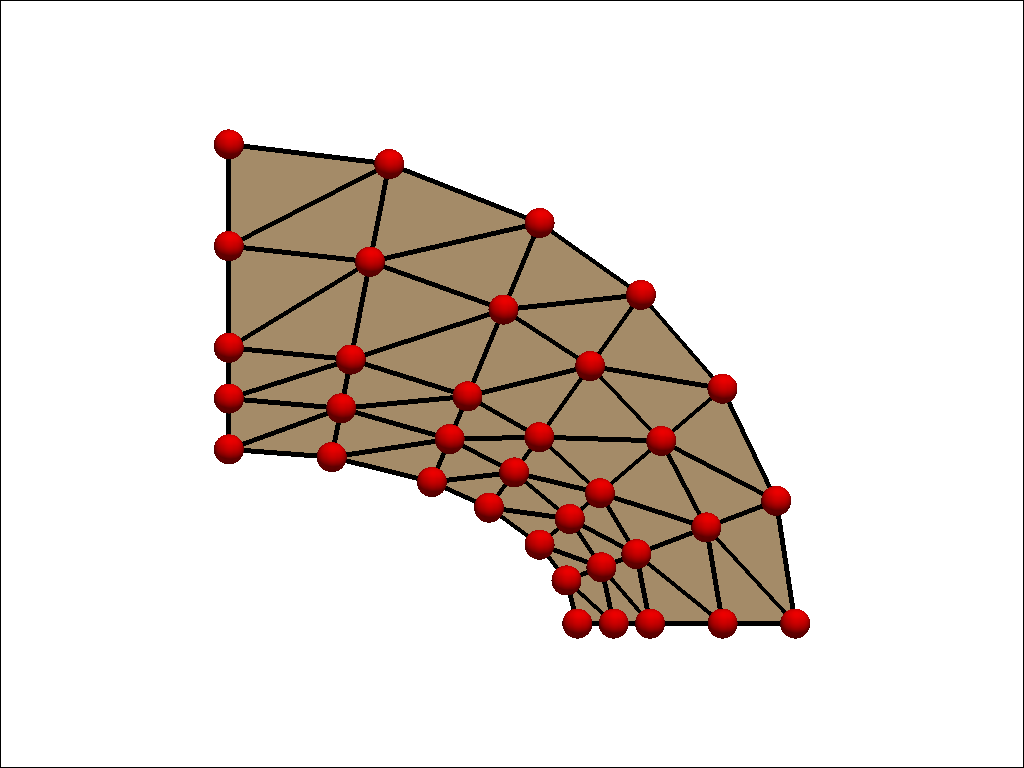
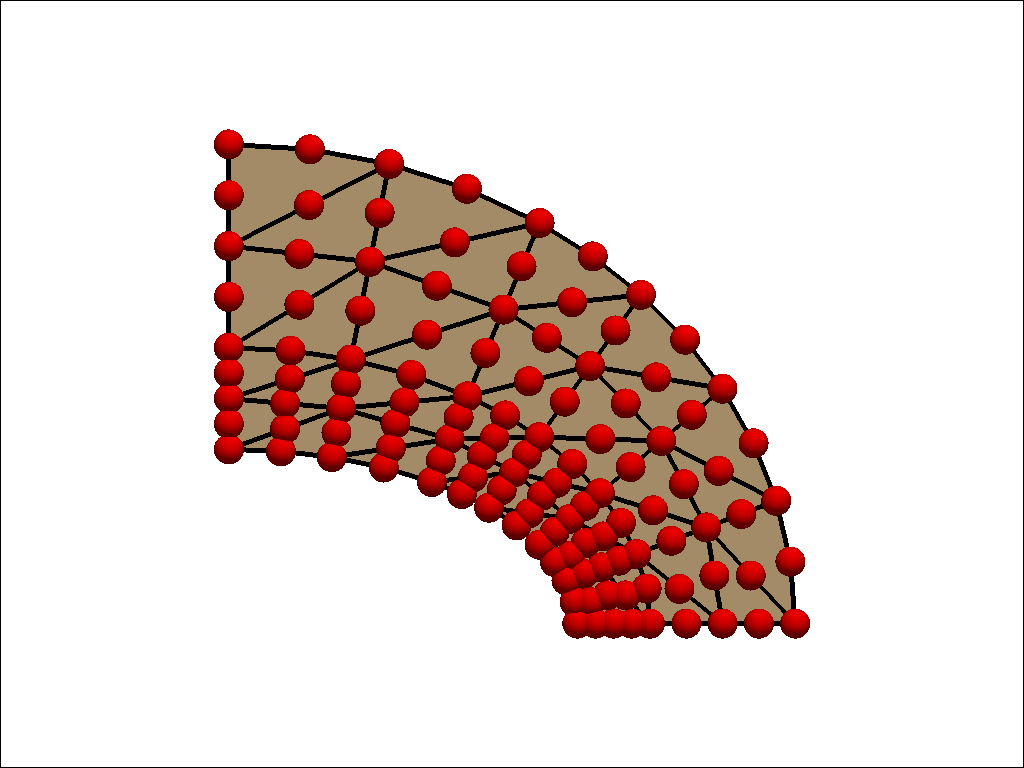
ベンチマークに使用するメッシュパターンは粗いメッシュと細いメッシュの2種類です。 使用した要素は1次要素、2次要素およびそれらの低減要素です。 粗いメッシュと細いメッシュ図は以下の通りです。
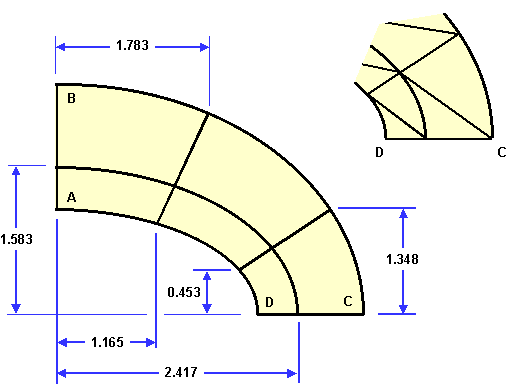
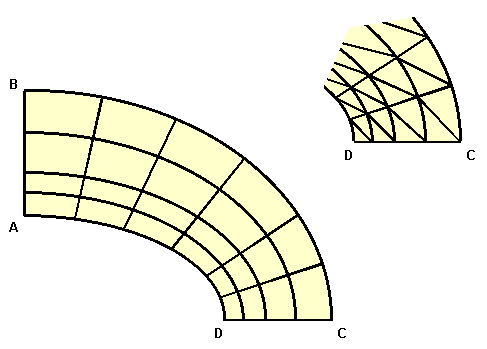
これらのメッシュをどのように作成しているかを説明します。 まず、GetFEMとNumPyをインポートして空の2次元メッシュを作成します。
1import getfem as gf
2import numpy as np
3
4mesh = gf.Mesh("empty", 2)
次に幾何変換のオブジェクトを定義します。
GT_QK(2,1) は2次元の1次4角形(quadrangle)幾何変換を表しています。
1gt = gf.GeoTrans("GT_QK(2,1)")
変数 x と変数 y に節点の座標を定義しておき要素の節点番号の構成を定義します。
1mesh.add_convex(gt, [[x[0], x[1], x[3], x[2]], [y[0], y[1], y[3], y[2]]])
2mesh.add_convex(gt, [[x[4], x[5], x[7], x[6]], [y[4], y[5], y[7], y[6]]])
3mesh.add_convex(gt, [[x[8], x[0], x[9], x[3]], [y[8], y[0], y[9], y[3]]])
4mesh.add_convex(gt, [[x[10], x[5], x[8], x[0]], [y[10], y[5], y[8], y[0]]])
5mesh.add_convex(gt, [[x[5], x[10], x[6], x[11]], [y[5], y[10], y[6], y[11]]])
6mesh.add_convex(gt, [[x[5], x[4], x[0], x[1]], [y[5], y[4], y[0], y[1]]])
メッシュはPyVistaを使用したPythonスクリプトで描画しています。
1import pyvista as pv
2
3pv.set_plot_theme("document")
4
5mesh = pv.read("coarse-quadrilateron-1d.vtk")
6
7plotter = pv.Plotter(border=True)
8
9plotter.add_mesh(mesh)
10plotter.add_mesh(
11 mesh.separate_cells().extract_feature_edges(),
12 show_edges=True,
13 line_width=5,
14 color="black",
15)
16plotter.add_points(
17 mesh.points, render_points_as_spheres=True, point_size=30.0, color="red"
18)
19
20plotter.show(cpos="xy", screenshot="coarse-quadrilateron-1d.png")
荷重の検討#
今回は検討として等価節点荷重の比較を行いました。
1md = gf.Model("real")
2md.add_fem_variable("u", mfu)
3md.add_initialized_fem_data("NeumannData", mfrhs, F)
4md.add_normal_source_term_brick(mim, "u", "NeumannData", OUTER_BOUND)
5# md.add_source_term(mim, "(Reshape(NeumannData,qdim(u),meshdim)*Normal).Test_u", OUTER_BOUND)
6md.assembly()
7RHS = md.rhs()
8print("RHS", RHS)
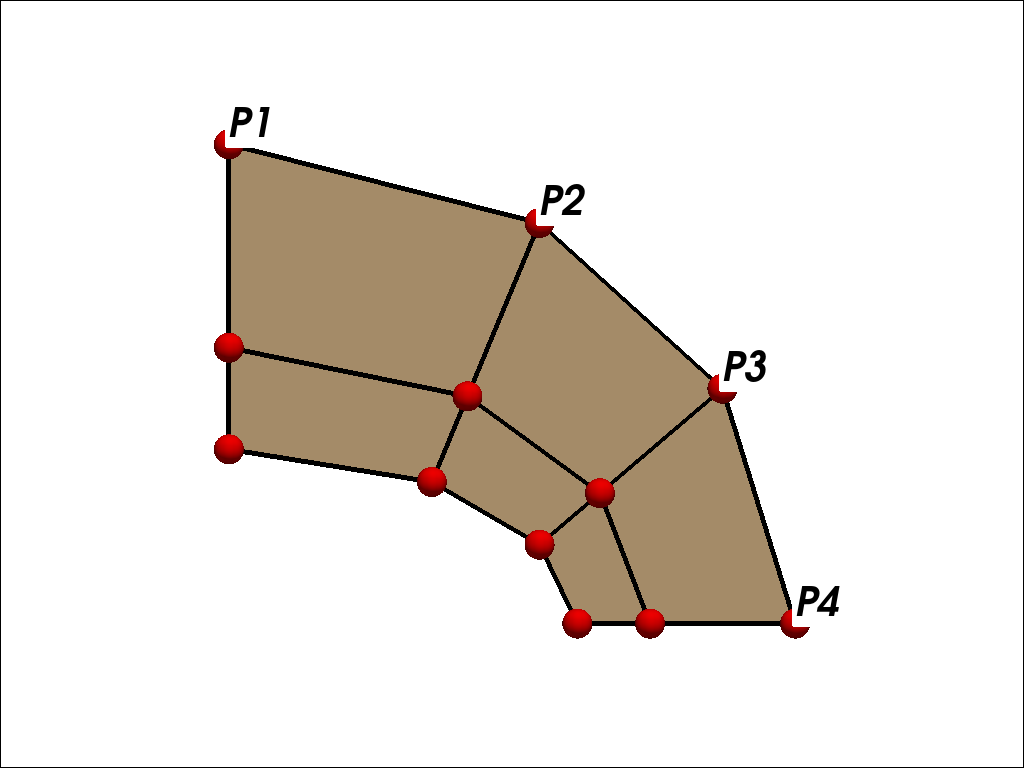
荷重負荷点 |
X方向荷重 |
参照値との相対誤差 |
Y方向荷重 |
参照値との相対誤差 |
|---|---|---|---|---|
P1 |
0.22539711 |
0.01% |
0.89149999 |
0.01% |
P2 |
0.70099997 |
0.00% |
1.41638279 |
0.01% |
P3 |
1.14960289 |
0.00% |
0.73350000 |
0.00% |
P4 |
0.67400002 |
0.00% |
0.20861721 |
0.00% |
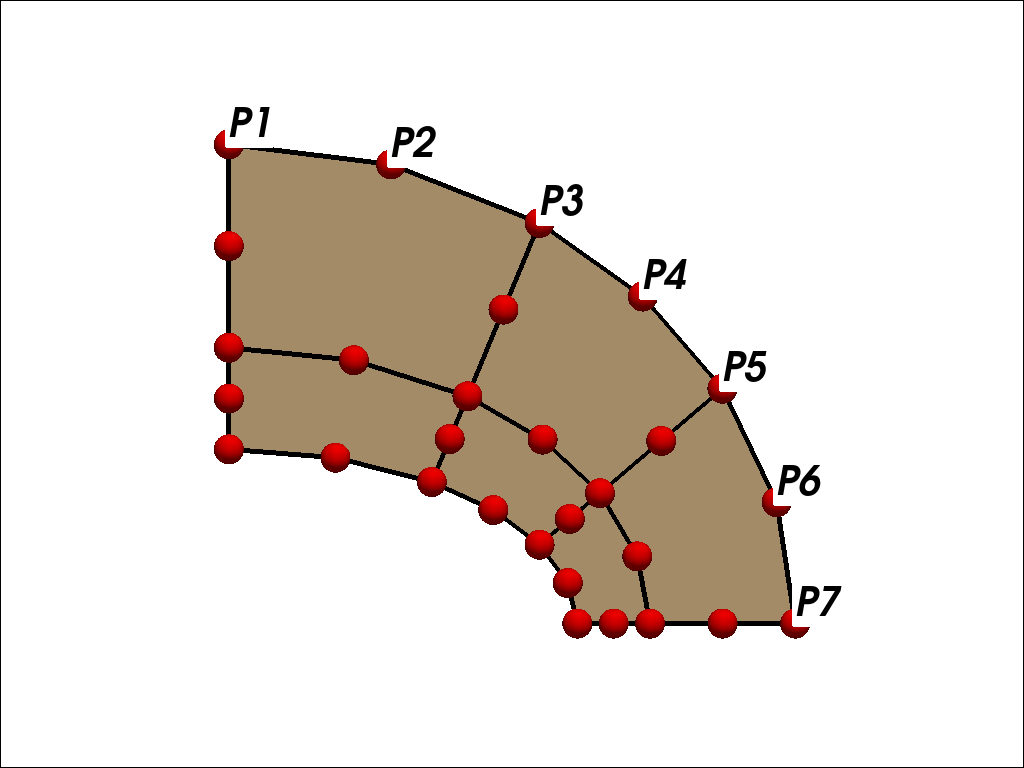
荷重負荷点 |
X方向荷重 |
参照値との相対誤差 |
Y方向荷重 |
参照値との相対誤差 |
|---|---|---|---|---|
P1 |
1.60599000e-03 |
97.88% |
3.23130648e-01 |
7.88% |
P2 |
3.00529480e-01 |
0.79% |
1.18866666e+00 |
0.79% |
P3 |
2.71656828e-01 |
13.35% |
4.91136831e-01 |
3.23% |
P4 |
6.34137153e-01 |
0.71% |
6.99843727e-01 |
0.71% |
P5 |
4.03582216e-01 |
4.34% |
2.67912545e-01 |
8.68% |
P6 |
8.98666700e-01 |
1.08% |
2.78156280e-01 |
1.08% |
P7 |
2.39821632e-01 |
5.59% |
1.15331000e-03 |
98.36% |
等価節点力の計算方法#
等価節点力は仮想変位 \(\delta u\left(\eta \right)\) と仮想仕事 \(\delta W\) の関係から計算されます。
ただし、 \(p\) は分布荷重の値、 \(h\) は要素厚さ \(\eta (0 \leqq \eta \leqq 1)\) は分布荷重が加わる面の接線方向座標とします。
1次要素の場合、変位は次の式で与えられます。
ただし、 \(u_1\) と \(u_2\) はそれぞれ \(\eta = 0\) と \(\eta = 1\) の節点における変位です。
この式を仮想変位の式に代入すると以下の式が得られます。
2次要素の場合、変位は次の式で与えられます。
ただし、 \(u_1\) と \(u_2\) と \(u_3\) はそれぞれ \(\eta = 0\) と \(\eta = \dfrac{1}{2}\) と \(\eta = 1\) の節点における変位です。
この式を仮想変位の式に代入すると以下の式が得られます。
以上で、分布荷重を求めることができました。 1次要素と2次要素いずれの場合もGetFEMで正しく等価節点力を求められることを確認しました。
まとめ#
GetFEMの機能を使用して The Standard NAFEMS Benchmarks のメッシュを作成できることを確認しました。
GetFEMを使用して等価節点荷重の値を計算しました。1次要素は参照値との相対誤差が0.01%以下でした。2次要素は参照値との相対誤差が0.50%以上98%以下でした。
等価節点力の計算方法について定式化を確認しました。
今後は単純なモデルで2次要素の等価節点荷重について確認をする予定です。 現在の定式化では分布荷重が一定となっていますがその部分をどう考えるかについて考察しています。 ご意見があればいただきたいです。